[ksnctf] MathⅠ

ksnctfにチャレンジ 第16問目です。

※ksnctfは常駐型のCTFサイトです。 ※問題のページはコチラです。

MathⅠ

RSA暗号に関する問題です。 RSA暗号は公開鍵暗号で、ある程度より大きな数を素因数分解するのは 大変だという数学上の問題を利用します。

1組の素数を使って 1組の暗号セット (e,n)と(d,n) を生成し pq:素数の組　M:平文　C:暗号文 とすると n = pq C = (M^e) mod n M = (C^d) mod n

で相互に変換できる　というものです。 肝心の e,d の生成方法は

Step1
 n = pq
 φ(n) = (p-1)(q-1)
 として
 eとφ(n)の最大公約数が1 になるような e を1つ探す
   ※eは公開鍵で固定値でも安全性に影響がないため
     e = 65537 がよく使われる
Step2
 １＝(de)modφ(n) となる d を見つける

こういう仕組みなので n がどの素数 p,q から生成されたか 因数分解できてしまうと　全部計算可能になってしまいますよ という話です。

本文はその p,q がなにかの表紙に特定できてしまったことを 想定して　暗号文C から　平文M を計算すればいいわけです。

p,q,e が分かっているので　d を計算できます。 ed ≡ 1 (modφ(n)) から ed = 1+kφ(n) de + k'φ(n) = 1 これは ax+by=1 の形のユークリッドの互除法で処理できます。

所謂拡張ユークリッドの互除法というアルゴリズムでは a,b に対して 　ax + by = gcd(a,b) となるような 　x,y gcd(a,b) が一気に求まります。

d が計算できたら　Cも計算できますが ここでちょっと問題があります。 ここで登場する c や d や n はかなり大きな値をとっているので c^d などの計算はそのままではできません。

そこで 巨大な値での冪剰余には 特別な配慮がいります。 が、そうそう思いつけるものもないので 参考 このあたりから持ってきました。

以上で M が計算できたので問題の指示にしたがって　デコードすればOKです。

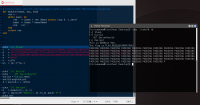
#!/usr/bin/ruby

class Euclid
    attr_reader :x
    attr_reader :y

    def initialize
        @x = 1
        @y = 0
    end

    def exgcd(a, b)
        x=1
        y=0
        u=0
        v=1

        while b>0 do
            q = a/b

             tmp = u
             u   = x-(q*u)
             x   = tmp

             tmp = v
             v   = y-(q*v)
             y   = tmp;

            tmp = b
            b   = a-(q*b)
            a   = tmp;
        end

        @x = x;
        @y = y;
        return a
    end
end

# https://docs.omniref.com/ruby/gems/rsa/0.1.2/symbols/RSA::Math/modpow/singleton
def moduler(base, exp, mod)
    res = 1
    while exp>0 do
        res   = (base * res )%mod unless (exp & 1).zero?
        base  = (base * base)%mod
        exp   >>= 1
    end
    return res
end

puts "[+] Steup"
c   = 225549592628492616152632265482125315868911125659971085929712296366214355608049224179339757637982541542745010822022226409126123627804953064072055667012172681551500780763483172914389813057444669314726404135978565446282309019729994976815925850916487257699707478206132474710963752590399332920672607440793116387051071191919835316845827838287954541558777355864714782464299278036910958484272003656702623646042688124964364376687297742060363382322519436200343894901785951095760714894439233966409337996138592489997024933882003852590408577812535049335652212448474376457015077047529818315877549614859586475504070051201054704954654093482056493092930700787890579346065916834434739980791402216175555075896066616519150164831990626727591876115821219941268309678240872298029611746575376322733311657394502859852213595389607239431585120943268774679785316133478171225719729917877009624611286702010936951705160870997184123775488592130586606070277173392647225589257616518666852404878425355285270687131724258281902727717116041282358028398978152480549468694659695121115046850718180640407034795656480263573773381753855724693739080045739160297875306923958599742379878734638341856117533253251168244471273520476474579680250862738227337561115160603373096699944163
p   = 34111525225922333955113751419357677129436029651245533697825114748126342624744832960936498161825269430327019858323450578875242014583535842110912370431931233957939950911741013017595977471949767235426490850284286661592357779825212265055931705799916913817655743434497422993498931394618832741336247426815710164342599150990608143637331068220244525541794855651643135012846039439355101027994945120698530177329829213208761057392236875366458197098507252851244132455996468628957560178868724310000317011912994632328371761486669358065577269198065792981537378448324923622959249447066754504943097391628716371245206444816309511381323
q   = 44481453884385518268018625442920628989497457642625668259648790876723318635861137128631112417617317160816537010595885992856520476731882382742220627466006460645416066646852266992087386855491152795237153901319521506429873434336969666536995399866125781057768075533560120399184566956433129854995464893265403724034960689938351450709950699740508459206785093693277541785285699733873530541918483842122691276322286810422297015782658645129421043160749040846216892671031156465364652681036828461619272427318758098538927727392459501761203842363017121432657534770898181975532066012149902177196510416802134121754859407938165610800223
e   = 65537
n   = p*q
pn  = (p-1)*(q-1)

puts "[+] Euclid"
puts " - GET SecretKey(d)"
euclid = Euclid.new()
euclid.exgcd(e,pn)
d = euclid.x + (e*pn)

puts "[+] Decrypt"
m   = moduler(c, d, n)
str = [sprintf("%0512x", m).to_s].pack('H*')